Conic Sections

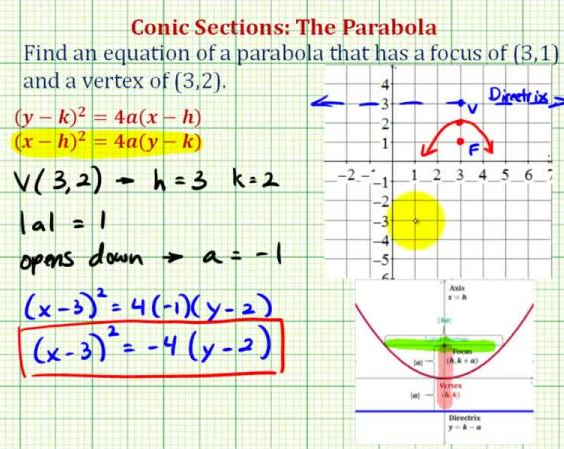
WOW! Class today was so interesting and fun. Miss V sure knows how to spice things up.....  Anyways, this lesson focuses specifically on conic section porabolas, a set of all points (x,y) that are equidistant from a fixed line (directrix) and a fixed  point (focus) not on the line. The midpoint between the focus and the directrix is called the vertex, and the line passing through the focus and the vertex is called the axis of the parabola. Using the definition of a parabola, you can derive the following standard form of the equation of a parabola whose directrix is parallel to the x-axis or to the y-axis. The vertex at (h,k), the standard form is: (x-h)^2 = 4p(y-k): vertical axis; directrix: y = k-p. (y-k)^2 = 4p(x-h): horizontal axis; directrix: x = h-p. The focus lies on the axis p units (directed distance) from the vertex. If the vertex is at the origin (0,0), the equation takes one of the following forms. x^2 = 4py: vertical axis. y^2 = 4px: horizontal axis. 

Here is an example of how to find the standard equation of a parabola:

Here is an illustration of how to find the focus:

And lastly a full example: