Once again our good friend teddy has imparted a special gift upon us. I don't know how to get rid of this underscore but whatever. Here we go teddy!
Elementary row options
1. Interchange two equations2 Multiply an equation by a nonzero equation
3. Add a multiple of an equation to another equation.
Row-echelon form: the necessary form we need for augmented matrices and system of equations.
1. Rows consisting of zeroes belong at the bottom
2. First nonzero has a 1
3. For each row the leading 1 in the higher row is to the left of the lower one.
Here are some examples of matrices in row-echelon form:
How to solve system of equations through Gaussian elimination with back substitution.
1. Get the matrix in row-echelon form using elementary row operations
2. Use back substitution to solve for each variable.
Gauss-Jordan elimination
1. Obtain the reduced row-echelon form using elementary row operations.
2. Variables are equal to the coefficients on the right.
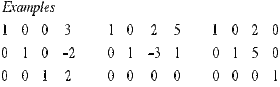
Nice notes. Thanks for sharing!
ReplyDeletematrices are really hard! good job on the notes aidaaan
ReplyDelete