Motorcycles

Recently my parents got me a motorcycle for my birthday and I've been having a lot of fun learning how to ride. That got me to thinking about what the fastest motorcycles in the world are and how fast they can accelerate. As it turns out, the fastest motorcycle in the world accelerates from 0-60 in 2.35 seconds. That is so dang fast. Apparently the fastest street legal motorcycle out right nown is the 2013 Ducati 1200 and it is recorded top speed at 210 mph. Blazing. We'll anyways I thought that was cool so here's a pic and a chart to add interest.

Time[note]	Make and model	Year (model)	Time (seconds)[note]
2.40	Suzuki GSX-R1000	2006	2.35[1] 2.8[2]
2.5	Yamaha VMAX	2010	2.5[3]
2.6	Kawasaki Ninja ZX-14R	2012	2.6[4]
2.70	BMW S1000RR	2011	2.70[5]
2.74	Suzuki Hayabusa	2010	2.74[6]
2.90	Ducati 999	2003	2.90[1]
2.9	Ducati Streetfighter 848	2012	2.9[7]
2.6	Ducati Diavel	2011	2.93[8][9]
3.3	Triumph Rocket III Roadster	2010	3.3[3]
3.44	Ducati Sport1000Biposto	2000	3.44[1]

Prezi

http://prezi.com/z5fbcpkcuxaw/chapter-8-vocabulary-hma/

Skydiving

One of my goals before I graduate is to go skydiving before I graduate. So, I decided it would be fun to look at the math behind it!

What happens when you jump out of a plane and then open a parachute? For Ivan Agudelo "the feeling is kind of like sticking your head out of the window of a car that is traveling at 100 miles per hour." And when the parachute opened Risa Centenni "...felt like a cork flying out of a bottle of champagne!" There must be some pretty strong forces at work to produce such intense feelings. Here's a closer look at the physics of skydiving.

Here is Philippe in free fall without a parachute. At this point the force of gravity is greater than the drag on his body so he is accelerating.

As he accelerates the amount of drag increases, because the faster an object moves through air, the greater the drag.

Eventually drag is equal to the force of gravity. He is no longer accelerating, but rather moving at a constant speed. He has reached terminal velocity, going as fast as he will go. This is roughly 200 kilometers per hour ( 125 miles per hour).

Making contact with the ground at that speed would be rather uncomfortable so Philippe opens his parachute.

With the parachute spread out above him rather than folded up tightly on his back, Philippe plus his parachute present a much larger surface area to the air they are moving through, greatly increasing drag. Since upward force is now greater than downward force, he suddenly begins to slow down. But as he moves slower and slower, drag decreases until...

...gravity and drag are once again equal and Philippe is again dropping at a constant velocity. But now that velocity is only about 22 kph (14 mph)...

...slow enough to make a happy landing.

 

Chapter 7 Review

I wasn't here all week so I just decided to make a review for chapter 7! So here it goes.

a) Substitution- substitute back into original equation
b) Elimination- eliminate until you are left with 1 variable that you can plug in
c) Break-Even Problems- memorize equations

d) Partial Decomposition- start with bottom and seperate then follow 7 steps 
e) Systems of 3 Equations- same as elimination keep plugging until you isolate 1 variable 
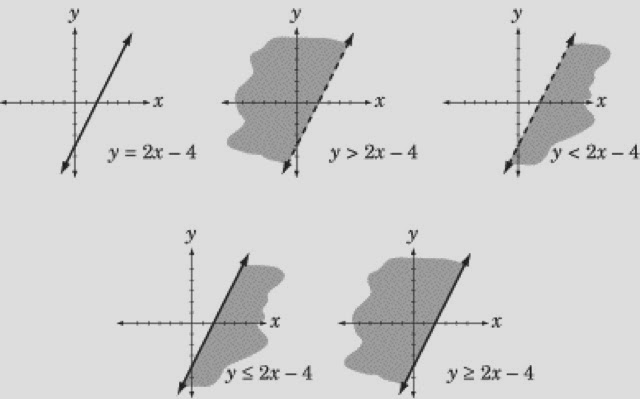
f) Linear Programming- know the signs of each graph.

Here are picture examples of each one.

Substitution

Elimination

Break even 

Partial Decomposition 

Fun Facts of Math

Last week, I read somebodies blog and really enjoyed reading all of there "fun facts of math." SOOO, I decided to be a copy cat and do the same thing. I think it's always very interesting when you can apply math to life and see how it work within the world. So, here I go.

1. π=3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 7816406286 20899 86280 34825 34211 70679 82148 08651 32823 ...
2. A sphere has two sides. However, there are one-sided surfaces.
3. There are shapes of constant width other than the circle. One can even drill square holes.
4. There are just five regular polyhedra
5. In a group of 23 people, at least two have the same birthday with the probability greater than 1/2
6. Everything you can do with a ruler and a compass you can do with the compass alone
7. Among all shapes with the same perimeter a circle has the largest area.
8. There are curves that fill a plane without holes
9. Much as with people, there are irrational, perfect, complex numbers
10. As in philosophy, there are transcendental numbers
11. As in the art, there are imaginary and surreal numbers
12. A straight line has dimension 1, a plane - 2. Fractals have mostly fractional dimension
13. You are wrong if you think Mathematics is not fun
14. Mathematics studies neighborhoods, groups and free groups, rings, ideals, holes, poles andremovable poles, trees, growth ...
15. Mathematics also studies models, shapes, curves, cardinals, similarity, consistency,completeness, space ...
16. Among objects of mathematical study are heredity, continuity, jumps, infinity,infinitesimals, paradoxes...
17. Last but not the least, Mathematics studies stability, projections and values, values are oftenabsolute but may also be extreme, local or global.
18. Trigonometry aside, Mathematics comprises fields like Game Theory, Braids Theory, Knot Theory and more
19. One is morally obligated not to do anything impossible
20. Some numbers are square, yet others are triangular
21. The next sentence is true but you must not believe it
22. The previous sentence was false
23. 12+3-4+5+67+8+9=100 and there exists at least one other representation of 100 with 9 digits in the right order and math operations in between
24. One can cut a pie into 8 pieces with three movements
25. Program=Algorithms+Data Structures
26. There is something the dead eat but if the living eat it, they die.
27. A clock never showing right time might be preferable to the one showing right time twice a day
28. Among all shapes with the same area circle has the shortest perimeter

Obviously I copy pasted this from a website but nonetheless is is very interesting. Number 24 is crazy. I have been thinking how to do it all day. Somebody comment with how to do it!

7.4 System of Inequalities

 ,I was not here for this lesson but Madie Johnson's kinder souls decided to help me out and share her notes with me and this is what a received from her graceful soul. 

Equation of a line: 

Y=mx+b

M=slope 

B=Y intercept 

Graph: a collection of all solutions of the inequality 

Dashed line: -for < or >

Dotted line: for _< or > 

Here is an example of graphing an inequality:

7.3 Partial Fractions

I was not in class much of the week so perhaps I missed out on some details... However, here are the steps to solving fractions that I have gathered from friends.

 

1) Factor Denominator

2) Place A over factor and B over factor

3) set the equation = A+B to the original equation 

4) Multiply everything by the GCF 

5) Cancel out what needs to be canceled out 

6) Distribute the A and B 

7) Group like terms together and factor out common variable 

8) Set equal to other side 

9) Use substitution or elimination to solve for x and y 

10) Plug back into original equation

Master Chef

About a week ago I was having a conversation with one of my old friends from middle school. As we were catching up on our lives we began to conversate about his dad; world class chef Joachim Spichal. As I began to as questions about his dad I was very interested in how he made his money. What my friend told me was very interesting.

Joachim Splichal, is a world renowned chef and also one of the 200 richest men in America. However, Mr. Splichal did not make his money the conventional way. He knew that creating a popular brand is the most important part of buisness. With this knowledge, he brilliantly devoted the early parts of his career to creating a name for himself. He did this by starting super fancy resturaunts with only the highest quality of foods. These resturaunts became so popular amongst the wealthy class that celebrities began to flock to his Patina resturaunt. His brand, Patina, began to make a name for itself. However, contrary to common thought, Mr. Splichal was not making money because the cost of his food (which was very high) did not equal the amount of revenue he was receiving. Therefore, he lost a lot of money during these years. This was all part of the plan though. Once he established himself as a major player in the food world he began to start small lower priced food resturaunts that did not have the high class food he was renowned for. However, because of his heralded "Patina" brand people came to the resturaunt in flocks. These small resturaunts is where he made his riches because the cost of his food was much less then the profit that he recieved. Mr. Splichal understood the concepts of break even and how to maximize his profits.

7.2 Elimination

Today we explored different ways to accomplish the same goals of solving two equations with two different variables. This is seen as an alternative root to substitution. There are 4 steps to this process.

1) obtain coefficients that differ only in sign.

2) add equations to eliminate a variable 

3) back substitute to solve for a second equation 

4) check you solution

Here is an example of how to do elimination. A few notes about the process:

1) it does not matter which equation you substitute back into. 

2) it does not matter which variable you decide to eliminate.

3) check using equation 1

We also learned how to do distance formulas while accounting for wind and the speed of the plain.the formulas for this was d=rt with the rate being p+w and p-w. you solve this just like an elimination formula! 

7.1 Substitution

Today we learned basic algebra concepts. The one thing I didn't know was that when you have x(x-2)=0 you can just separate x and x-2 into two separate entities and solve each one individually. Also there are situations were there are no solutions. Also we learned how to gage profit and how to break even. The key equation is that total cost = total revenue in order to break even. One questions had was what the initial cost was and it is explained as the money needed in order to start or make the product.

 

This is a graph of break even and it illustrates how the cost is equal to the revenue when they are equal. Similarly, profit is made when cost<revenue. Money is lot when cost>revenue.